সমবাহু ত্রিভুজ কাকে বলে | সমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র
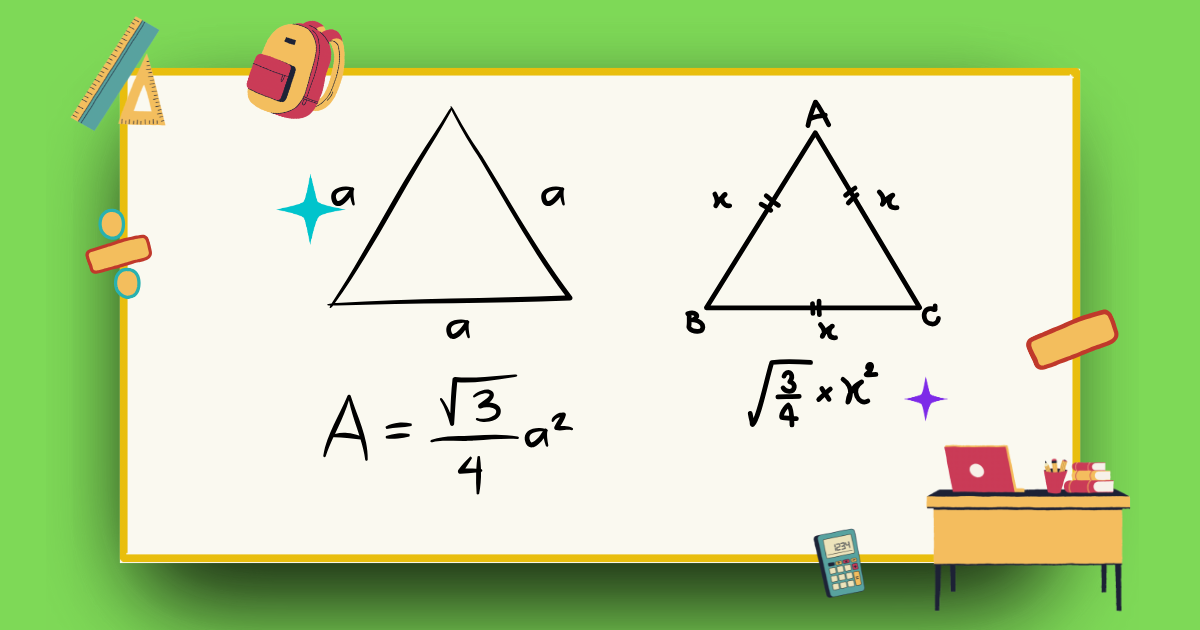
সমবাহু ত্রিভুজ কাকে বলে
সমবাহু ত্রিভুজ (Equilateral Triangle) হলো এমন একটি ত্রিভুজ যার তিনটি বাহু সমান দৈর্ঘ্যের এবং তিনটি কোণই সমান। প্রতিটি কোণের মান ৬০° হওয়ায়, এটি জ্যামিতিক গঠন এবং গাণিতিক গবেষণায় গুরুত্বপূর্ণ ভূমিকা পালন করে। সমবাহু ত্রিভুজে যেকোনো কোণ থেকে বিপরীত বাহুতে আঁকা উচ্চতা, মধ্যমা এবং প্রতিসাম্য রেখাগুলি এক বিন্দুতে মিলিত হয়, যা ত্রিভুজের কেন্দ্রে অবস্থিত।
সমবাহু ত্রিভুজের বৈশিষ্ট্য
সমবাহু ত্রিভুজের কিছু গুরুত্বপূর্ণ বৈশিষ্ট্য আছে, যা অন্যান্য ত্রিভুজ থেকে এটিকে আলাদা করে তোলে:
- তিনটি বাহু সমান দৈর্ঘ্যের হয়।
- তিনটি কোণই সমান এবং প্রতিটির মান ৬০°।
- ত্রিভুজের তিনটি প্রতিসাম্য রেখা থাকে, যা একটি কেন্দ্রে মিলিত হয় এবং এই কেন্দ্রটি ত্রিভুজের চারিত্রিক কেন্দ্র হিসেবে বিবেচিত।
- সমবাহু ত্রিভুজে উচ্চতা, মধ্যমা এবং প্রতিসাম্য রেখা একই স্থানে মিলিত হয়, যা অন্যান্য ত্রিভুজে সাধারণত দেখা যায় না।
সমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র
সমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয় করার জন্য সাধারণত নিচের সূত্রটি ব্যবহৃত হয়, যা সহজেই এর বাহুর দৈর্ঘ্য অনুযায়ী ক্ষেত্রফল বের করতে সহায়ক:
- ক্ষেত্রফল: \( \text{Area} = \frac{\sqrt{3}}{4} \times a^2 \)
এখানে \( a \) হলো ত্রিভুজের একটি বাহুর দৈর্ঘ্য। উদাহরণস্বরূপ, যদি একটি সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য ৬ সেমি হয়, তবে এর ক্ষেত্রফল হবে \( \frac{\sqrt{3}}{4} \times 6^2 = 15.59 \) বর্গ সেমি। এটি ত্রিভুজের অভ্যন্তরীণ এলাকা নির্ধারণ করে, যা বিভিন্ন ক্ষেত্রে যেমন স্থাপত্য এবং প্রকৌশলে গুরুত্বপূর্ণ ভূমিকা পালন করে।
সমবাহু ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র
সমবাহু ত্রিভুজের পরিসীমা বের করার জন্য নিচের সূত্রটি ব্যবহৃত হয়। পরিসীমা হলো ত্রিভুজের বাহুগুলির সমষ্টি:
- পরিসীমা: \( \text{Perimeter} = 3 \times a \)
যদি একটি সমবাহু ত্রিভুজের প্রতিটি বাহু ৮ সেমি হয়, তাহলে পরিসীমা হবে \( 3 \times 8 = 24 \) সেমি। এটি ত্রিভুজের বাইরের সীমানা প্রকাশ করে এবং সাধারণত ত্রিভুজের সম্পূর্ণ দৈর্ঘ্য নির্ধারণে সহায়ক।
সমবাহু ত্রিভুজের উচ্চতা নির্ণয়ের সূত্র
সমবাহু ত্রিভুজের উচ্চতা বের করার জন্য নিচের সূত্রটি ব্যবহার করা হয়। উচ্চতা ত্রিভুজের শীর্ষ বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দুতে আঁকা হয় এবং এটি একটি প্রধান গাণিতিক গঠন প্রদান করে:
- উচ্চতা: \( h = \frac{\sqrt{3}}{2} \times a \)
যেখানে \( a \) হলো ত্রিভুজের একটি বাহুর দৈর্ঘ্য। উদাহরণস্বরূপ, যদি বাহুর দৈর্ঘ্য ১০ সেমি হয়, তবে উচ্চতা হবে \( \frac{\sqrt{3}}{2} \times 10 = 8.66 \) সেমি। উচ্চতা ত্রিভুজের আয়তন এবং অন্যান্য গাণিতিক গঠন নির্ধারণে সহায়ক ভূমিকা পালন করে।
সমবাহু ত্রিভুজের মধ্যমা নির্ণয়ের সূত্র
সমবাহু ত্রিভুজের প্রতিটি মধ্যমা সমান দৈর্ঘ্যের হয় এবং নিচের সূত্রে নির্ণয় করা হয়। মধ্যমা হলো ত্রিভুজের একটি শীর্ষবিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দুতে যাওয়া রেখা:
- মধ্যমা: \( \text{Median} = \frac{\sqrt{3}}{2} \times a \)
যদি একটি ত্রিভুজের বাহু ৭ সেমি হয়, তবে মধ্যমার দৈর্ঘ্য হবে \( \frac{\sqrt{3}}{2} \times 7 = 6.06 \) সেমি। মধ্যমার সাহায্যে আমরা ত্রিভুজের মধ্যবিন্দু নির্ধারণ করতে পারি, যা জ্যামিতিক ক্ষেত্রে অত্যন্ত গুরুত্বপূর্ণ।
সমবাহু ত্রিভুজের প্রতিসাম্য রেখা কয়টি
সমবাহু ত্রিভুজে তিনটি প্রতিসাম্য রেখা থাকে, যা প্রতিটি শীর্ষবিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দুতে মিলিত হয়। প্রতিসাম্য রেখাগুলি ত্রিভুজের কেন্দ্রে মিলে ত্রিভুজের গঠনকে একটি স্বতন্ত্র সৌন্দর্য প্রদান করে।
সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ নির্ণয়ের সূত্র
সমবাহু ত্রিভুজের চারপাশে অঙ্কিত পরিবৃত্তের ব্যাসার্ধ নির্ণয়ের জন্য নিচের সূত্রটি ব্যবহৃত হয়:
- পরিবৃত্তের ব্যাসার্ধ: \( R = \frac{a}{\sqrt{3}} \)
এখানে \( a \) হলো ত্রিভুজের একটি বাহু। উদাহরণস্বরূপ, যদি বাহুর দৈর্ঘ্য ১২ সেমি হয়, পরিবৃত্তের ব্যাসার্ধ হবে \( \frac{12}{\sqrt{3}} = 6.93 \) সেমি। এটি ত্রিভুজের পরিধি ও কেন্দ্রের সাথে সম্পর্ক স্থাপন করে।
সমবাহু ত্রিভুজের প্রতিটি কোণের মান কত
সমবাহু ত্রিভুজের প্রতিটি কোণ সমান এবং প্রতিটি কোণের মান ৬০°। ত্রিভুজের মোট কোণ যোগফল ১৮০° হওয়ায়, প্রতিটি কোণ সমানভাবে ৬০° হয়। এই কোণের মানের সাহায্যে সমবাহু ত্রিভুজের গঠন সহজে বিশ্লেষণ করা যায়।
উপসংহার
সমবাহু ত্রিভুজের বৈশিষ্ট্য, ক্ষেত্রফল, পরিসীমা, উচ্চতা, এবং প্রতিসাম্য নির্ণয়ের বিভিন্ন সূত্র শিক্ষার্থীদের জন্য বিশেষ গুরুত্বপূর্ণ। এই সূত্রগুলি জ্যামিতিক গঠন ও পরিমাপের ক্ষেত্রে নানা কাজে আসে এবং সমবাহু ত্রিভুজ সম্পর্কে গভীর জ্ঞান অর্জনে সহায়ক। শিক্ষার্থীরা গণিত পরীক্ষায় ভালো নম্বর পাওয়ার জন্য এগুলোকে সহজে শিখতে ও প্রয়োগ করতে পারেন।
- Education
- Health
- Lifestyle
- Job
- Visa
- Govt Info
- Career
- Tech
- Art
- Causes
- Crafts
- Dance
- Drinks
- Film
- Fitness
- Food
- Games
- Gardening
- Health
- Home
- Literature
- Music
- Networking
- Other
- Party
- Religion
- Shopping
- Sports
- Theater
- Wellness

